
Ashwood, Melbourne, Australia (2010–11); Washington, DC, United States (2021–22)
(posted February 26, 2011; updated April 6, 2021)
Abstract
Many edge detection algorithms use the Sobel, Scharr, Prewitt, or Roberts-cross operator for estimating the components of the gradient of the image. I introduce a new gradient operator that has resolution and fidelity that is superior to these operators.
Estimating the gradient of an signal is a fundamental task in any field of numerical computing. If the signal is sampled on a regular lattice, as it is in pixmaps or voxmaps, then the first-principles definition of differentiation leads to the naive solution of simply taking the first-difference of the signal in the direction desired. For example, if s(i) is a signal on a one-dimensional lattice, where i = 0, 1, 2, ... , and c is the lattice spacing, then [s(i+1) - s(i)] / c is a naive estimate of the derivative (gradient).
The problem arises when there is more than one dimension, as in the practically important case of pixmap images. For example, if we want to combine the two components of the gradient of a two-dimensional image—say, to find the magnitude of the gradient, or its direction—we need to know precisely where those gradient estimates are located. Consider: using the naive definition, the gradient in the x-direction can be defined as Gx = [s(i+1, j) - s(i, j)] / c, and the gradient in the y-direction can be defined as Gy = [s(i, j+1) - s(i, j)] / c. (Let’s assume that the lattice spacing is the same, c, in each direction.) The problem is that Gx is estimating the x-gradient half-way between columns i and i+1, and Gy is estimating the y-gradient half-way between rows j and j+1. In other words, the naive Gx and Gy are on different spatial lattices, and so cannot be directly combined.
The standard solution to this problem is to use the “central difference” operator, [s(i+1) - s(i-1)] / 2c, in each direction, for which the gradient estimate is located right on the central lattice site i. We can then combine x and y gradients, as they are defined on the same lattice. (It is understood that one row or column is omitted from each edge of the pixmap, as no signal is available for pixels outside the pixmap.)
The problem now, however, is that the response of this operator to sharp edges has been smudged out across three lattice sites. If a similar blurring is not applied in the orthogonal direction, then the x and y components of sharp corners will fail to be correctly co-located.
The standard solution to this problem is to use Sobel blurring kernel, which is a kernel of {1/4, 1/2, 1/4} in the orthogonal direction. (The Sobel operator is the combination of the Sobel blurring kernel and the central difference operator.) More recent variants are the Scharr blurring kernel, {3/16, 5/8, 3/16}, which improves rotational invariance, and the Prewitt blurring kernel of {1/3, 1/3, 1/3}.
A more ingenious method is the Roberts cross, which effectively looks at the pixmap on a 45-degree angle, and uses the naive difference operator. Defining G+ = [s(i+1, j+1) - s(i, j)] / c√2 and G- = [s(i+1, j) - s(i+1, j)] / c√2, we see that G+ measures the gradient in the x = y direction, and G- measures it in the x = -y direction. More importantly, both are defined on lattices that are half-way between the original lattice positions in both, and so they can be combined together.
These historical solutions suffer from the fact that they have lower inherent resolution than the pixmap they are differencing: the Sobel, Scharr, and Prewitt operators have half the resolution in each direction, and the Roberts cross has 1/√2 of the resolution in each direction. Fourier theory tells us that components of the original image that have a higher frequency than these cutoffs will be aliased in the gradient image. The net result is that they have lower resolution than the original image, as well as aliasing artifacts.
The gradient operator that I will now put forward returns to the original naive first-difference gradient operator, and solves its half-lattice-site offset problem in a different way.
The key to the solution is to use the gold standard Magic Kernel Sharp algorithm to “double” the image, i.e. upsample it with twice as many pixel tiles in each dimension as the original, with the default behavior that the left edge of the first upsampled pixel tile aligns with that of the first original pixel tile, etc.; i.e. the upsampled pixel centers are not coincident with the original pixel centers. It is straightforward to see that if we use the naive differencing operator in the x-direction, double once (in both directions) using Magic Kernel Sharp, and then discard the top and bottom rows of the result, we obtain an x-gradient pixmap of twice the resolution of the original image, in which the lattice positions are identical to those of the y-gradient pixmap obtained in the same manner.
The results are best appreciated with a practical example.
Consider the following image, taken from the Wikipedia pages on edge detection:

Original image
For visual comparison purposes only, we can upsample this original image by a factor of 2 using Magic Kernel Sharp:

Original image upsampled by a factor of 2
The magnitude of the gradient of the original image estimated by the proposed operator is:

Proposed operator
The Sobel operator yields (upsampled to the same scale for visual purposes):

Sobel operator
The Scharr operator yields:

Scharr operator
The Prewitt operator yields:

Prewitt operator
Finally, the Roberts-cross operator yields:

Roberts-cross operator
A more direct visual comparison can be made by focusing on the portion of this image with the most detail:

Original
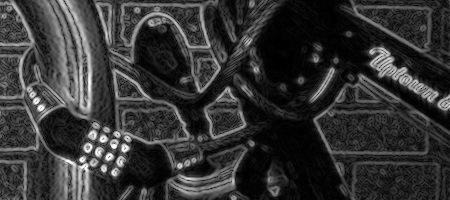
Proposed

Sobel

Scharr

Prewitt

Roberts-cross
Zooming in on the “Uptown” label (800% original size):

Original

Proposed

Sobel

Scharr

Prewitt

Roberts-cross
It can be seen that the Sobel, Scharr, and Prewitt operators suffer significantly, both from the orthogonal blurring kernel that they employ, yielding both poorer resolution, as well as significant aliasing artifacts between closely adjacent edges (particularly the cross-hatching artifact) due to the deficient Fourier properties of the central difference operator. The performance of the Roberts-cross operator is slightly superior to these operators but inferior to the new operator, reflecting its intermediate resolution.
The reference implementation of the Magic Edge Detector described above is contained in the following ANSI C code:
There is one sample program included:
There are also 80 executables of unit tests and death tests provided.
Instructions for building the code are contained in the _README file within the archive.
Note that all code provided here is from my personal codebase, and is supplied under the MIT License.
If you like the Magic Edge Detector, then you may also find useful the following image processing resources that I have put into the public domain over the decades:
© 2011–2024 John Costella